ປະຫວັດຄວາມເປັນມາ
ກະດາດນີ້ທົດລອງນໍາໃຊ້ວິທີການ heuristic ທີ່ແຕກຕ່າງກັນກັບບັນຫາການຈັດວາງສະຖານທີ່ທີ່ແທ້ຈິງຢູ່ໃນບໍລິສັດຜະລິດເຟີນີເຈີ. ແບບຈໍາລອງທັງຫມົດຖືກປຽບທຽບໂດຍໃຊ້ AHP, ບ່ອນທີ່ມີຕົວກໍານົດການທີ່ຫນ້າສົນໃຈຫຼາຍ. ການທົດລອງສະແດງໃຫ້ເຫັນວ່າວິທີການສ້າງແບບຈໍາລອງຮູບແບບຢ່າງເປັນທາງການສາມາດຖືກນໍາໃຊ້ຢ່າງມີປະສິດທິພາບໃນບັນຫາທີ່ແທ້ຈິງທີ່ປະເຊີນຫນ້າໃນອຸດສາຫະກໍາ, ນໍາໄປສູ່ການປັບປຸງທີ່ສໍາຄັນ.
1. ພາກສະເຫນີ
ອຸດສາຫະກໍາເຟີນີເຈີກໍາລັງປະສົບກັບຍຸກທີ່ມີການແຂ່ງຂັນຫຼາຍຄືກັບຄົນອື່ນ, ດັ່ງນັ້ນຈຶ່ງພະຍາຍາມຢ່າງຫນັກຫນ່ວງໃນການຄົ້ນຫາວິທີການຫຼຸດຜ່ອນຄ່າໃຊ້ຈ່າຍໃນການຜະລິດ, ປັບປຸງຄຸນນະພາບແລະອື່ນໆ. ເປັນສ່ວນຫນຶ່ງຂອງໂຄງການປັບປຸງຜະລິດຕະພັນໃນບໍລິສັດຜະລິດໃນນີ້ເອີ້ນວ່າ (ບໍລິສັດ = TC) ພວກເຮົາໄດ້ດໍາເນີນໂຄງການເພື່ອເພີ່ມປະສິດທິພາບການອອກແບບຮູບແບບຂອງສາຍການຜະລິດຢູ່ຊັ້ນຮ້ານຂອງບໍລິສັດນີ້ເພື່ອແນໃສ່ເອົາຊະນະບັນຫາໃນປະຈຸບັນທີ່ມີປະສິດຕິຜົນ. ມັນໄດ້ຖືກຕັດສິນໃຈທີ່ຈະນໍາໃຊ້ເຕັກນິກການສ້າງແບບຈໍາລອງຮູບແບບຈໍານວນຫນຶ່ງເພື່ອສ້າງຮູບແບບທີ່ເຫມາະສົມທີ່ໃກ້ຄຽງໂດຍອີງໃສ່ວິທີການທີ່ເປັນທາງການທີ່ບໍ່ຄ່ອຍຖືກນໍາໃຊ້ໃນການປະຕິບັດ. ເຕັກນິກການສ້າງແບບຈໍາລອງທີ່ໃຊ້ແມ່ນທິດສະດີກາຟ, ແຜນ Bloc, CRAFT, ລໍາດັບທີ່ດີທີ່ສຸດແລະສູດການຄິດໄລ່ທາງພັນທຸກໍາ. ຫຼັງຈາກນັ້ນ, ການຈັດວາງເຫຼົ່ານີ້ໄດ້ຖືກປະເມີນແລະປຽບທຽບໂດຍໃຊ້ 3 ເງື່ອນໄຂຄື: ພື້ນທີ່ລວມ, ການໄຫຼ * ຫ່າງແລະອັດຕາສ່ວນທີ່ຢູ່ໃກ້ຄຽງ. Total Area ໝາຍເຖິງເຂດທີ່ຄອບຄອງໂດຍສາຍການຜະລິດຂອງແຕ່ລະແບບທີ່ໄດ້ພັດທະນາ. Flow * Dist ຄິດໄລ່ຜົນລວມຂອງຜະລິດຕະພັນຂອງການໄຫຼເຂົ້າແລະໄລຍະຫ່າງລະຫວ່າງທຸກໆ 2 ສະຖານທີ່. Adjacency Percentage ຄິດໄລ່ອັດຕາສ່ວນຂອງສິ່ງອໍານວຍຄວາມສະດວກທີ່ຕອບສະຫນອງຄວາມຕ້ອງການທີ່ຢູ່ຕິດກັນ.
ການຄັດເລືອກຮູບແບບທີ່ດີທີ່ສຸດແມ່ນເຮັດໄດ້ຢ່າງເປັນທາງການໂດຍການນໍາໃຊ້
ຄໍານິຍາມຂອງບັນຫາການຈັດວາງຂອງພືດແມ່ນເພື່ອຊອກຫາການຈັດລຽງທີ່ດີທີ່ສຸດຂອງສິ່ງອໍານວຍຄວາມສະດວກທາງດ້ານຮ່າງກາຍເພື່ອໃຫ້ການດໍາເນີນງານທີ່ມີປະສິດທິພາບ (Hassan and Hogg, 1991). ຮູບລັກທີ່ມີຜົນກະທົບຄ່າໃຊ້ຈ່າຍຂອງການຈັດການອຸປະກອນການ, ການນໍາໃຊ້ເວລາແລະ throughput. ດັ່ງນັ້ນ, ມັນສົ່ງຜົນກະທົບຕໍ່ຜົນຜະລິດລວມແລະປະສິດທິພາບຂອງພືດ. ອີງຕາມການ Tompkins and White (1984) ການອອກແບບຂອງສິ່ງອໍານວຍຄວາມສະດວກແມ່ນໄດ້ປະມານຕະຫຼອດປະຫວັດສາດທີ່ບັນທຶກໄວ້ແລະຕົວຈິງແລ້ວສິ່ງອໍານວຍຄວາມສະດວກໃນຕົວເມືອງທີ່ຖືກອອກແບບແລະກໍ່ສ້າງໄດ້ຖືກອະທິບາຍໄວ້ໃນວັດຖຸບູຮານ.
* ຜູ້ຂຽນທີ່ສອດຄ້ອງກັນ
ປະຫວັດສາດຂອງປະເທດເກຣັກແລະ Empire Roman. ໃນບັນດາຜູ້ທີ 1 ຜູ້ທີ່ໄດ້ສຶກສາບັນຫານີ້ແມ່ນ Armor ແລະ Buffa et al. (1964). ເບິ່ງຄືວ່າພຽງເລັກນ້ອຍໄດ້ຮັບການຈັດພີມມາໃນປີ 1950. Francis and White (1974) ແມ່ນຜູ້ທີ 1 ທີ່ເກັບກໍາແລະປັບປຸງການຄົ້ນຄວ້າເບື້ອງຕົ້ນກ່ຽວກັບພື້ນທີ່ນີ້. ການຄົ້ນຄວ້າຕໍ່ມາໄດ້ຖືກປັບປຸງໂດຍ 2 ການສຶກສາທີ່ 1 ໂດຍ Domschke ແລະ Drexl (1985) ແລະອີກອັນຫນຶ່ງໂດຍ Francis et al. (1992). Hassan and Hogg (1991) ລາຍງານການສຶກສາຢ່າງກວ້າງຂວາງກ່ຽວກັບປະເພດຂອງຂໍ້ມູນທີ່ຕ້ອງການໃນບັນຫາການຈັດວາງເຄື່ອງຈັກ. ຂໍ້ມູນການຈັດວາງເຄື່ອງແມ່ນພິຈາລະນາເປັນລໍາດັບ; ຂຶ້ນຢູ່ກັບລາຍລະອຽດຂອງການຈັດວາງໄດ້ຖືກອອກແບບ. ໃນເວລາທີ່ຮູບແບບທີ່ຕ້ອງການແມ່ນພຽງແຕ່ເພື່ອຊອກຫາການຈັດລຽງຂອງເຄື່ອງຈັກ, ຂໍ້ມູນຕົວແທນຈໍານວນເຄື່ອງແລະຄວາມສໍາພັນການໄຫຼຂອງເຂົາເຈົ້າແມ່ນພຽງພໍ. ຢ່າງໃດກໍຕາມ, ຖ້າຮູບແບບລະອຽດແມ່ນຕ້ອງການ, ຕ້ອງການຂໍ້ມູນເພີ່ມເຕີມ. ໃນການຊອກຫາຂໍ້ມູນຄວາມຫຍຸ້ງຍາກບາງຢ່າງອາດຈະເກີດຂຶ້ນໂດຍສະເພາະແມ່ນໃນສະຖານທີ່ການຜະລິດໃຫມ່ທີ່ຍັງບໍ່ມີຂໍ້ມູນ. ເມື່ອຮູບແບບໄດ້ຖືກພັດທະນາສໍາລັບສິ່ງອໍານວຍຄວາມສະດວກທີ່ທັນສະໄຫມແລະອັດຕະໂນມັດ, ຂໍ້ມູນທີ່ຕ້ອງການບໍ່ສາມາດໄດ້ຮັບຈາກຂໍ້ມູນປະຫວັດສາດຫຼືຈາກສິ່ງອໍານວຍຄວາມສະດວກທີ່ຄ້າຍຄືກັນເພາະວ່າພວກມັນອາດຈະບໍ່ມີຢູ່. ການສ້າງແບບຈໍາລອງທາງຄະນິດສາດໄດ້ຖືກແນະນໍາວ່າເປັນວິທີທີ່ຈະໄດ້ຮັບການແກ້ໄຂທີ່ດີທີ່ສຸດສໍາລັບບັນຫາການຈັດວາງສະຖານທີ່. ນັບຕັ້ງແຕ່ຮູບແບບຄະນິດສາດທີ 1 ພັດທະນາໂດຍ Koopmans ແລະ Beckmann (1957) ເປັນບັນຫາການມອບຫມາຍສີ່ຫລ່ຽມ, ຄວາມສົນໃຈໃນພື້ນທີ່ໄດ້ດຶງດູດການຂະຫຍາຍຕົວຢ່າງຫຼວງຫຼາຍ. ນີ້ໄດ້ເປີດພື້ນທີ່ໃຫມ່ແລະຫນ້າສົນໃຈສໍາລັບນັກຄົ້ນຄວ້າ. ໃນການຊອກຫາວິທີການແກ້ໄຂບັນຫາຮູບແບບສິ່ງອໍານວຍຄວາມສະດວກ, ນັກຄົ້ນຄວ້າໄດ້ເປີດຕົວຕົວເອງໃນການພັດທະນາແບບຈໍາລອງທາງຄະນິດສາດ. Houshyar and White (1993) ເບິ່ງບັນຫາການຈັດວາງເປັນ
ສີຂຽວແລະ
2. ວິທີການສ້າງແບບຈໍາລອງ
ແບບຈໍາລອງໄດ້ຖືກຈັດປະເພດຂຶ້ນກັບລັກສະນະຂອງມັນ, ສົມມຸດຕິຖານແລະຈຸດປະສົງ. ວິທີການວາງແຜນການຈັດວາງລະບົບທົ່ວໄປທີ 1, ພັດທະນາໂດຍ Muthor (1955), ຍັງເປັນໂຄງການທີ່ເປັນປະໂຫຍດໂດຍສະເພາະຖ້າໄດ້ຮັບການສະຫນັບສະຫນູນຈາກວິທີການອື່ນໆແລະການຊ່ວຍເຫຼືອໂດຍຄອມພິວເຕີ. ວິທີການກໍ່ສ້າງ, Hassan and Hogg (1991) ສໍາລັບການຍົກຕົວຢ່າງ, ການກໍ່ສ້າງຮູບແບບຈາກ scratch ໃນຂະນະທີ່ວິທີການປັບປຸງ, Bozer, Meller and Erlebacher (1994) ສໍາລັບການຍົກຕົວຢ່າງ, ພະຍາຍາມດັດແປງຮູບແບບທີ່ມີຢູ່ແລ້ວສໍາລັບຜົນໄດ້ຮັບທີ່ດີກວ່າ. ວິທີການເພີ່ມປະສິດທິພາບແລະຍັງ heuristics ສໍາລັບການຈັດວາງໂດຍແມ່ນເປັນເອກະສານທີ່ດີໂດຍ Heragu (2007).
ເຕັກນິກການສ້າງແບບຈໍາລອງຕ່າງໆທີ່ໃຊ້ໃນວຽກງານນີ້ແມ່ນທິດສະດີກາຟ, CRAFT, ລໍາດັບທີ່ດີທີ່ສຸດ, BLOCPLAN ແລະສູດການຄິດໄລ່ທາງພັນທຸກໍາ. ອະທິບາຍຂ້າງລຸ່ມນີ້ແມ່ນຕົວກໍານົດການທີ່ຕ້ອງການໂດຍແຕ່ລະ algorithm ເພື່ອສ້າງແບບຈໍາລອງດຽວກັນ.
ທິດສະດີກາຟິກ
ທິດສະດີກຣາຟ (Foulds and Robinson, 1976; Giffin et al., 1984; Kim and Kim, 1985; ແລະ Leung, 1992) ນຳໃຊ້ເປັນ
ເອກະສານສະບັບນີ້ໃຊ້ 2 ວິທີການທີ່ແຕກຕ່າງກັນເພື່ອສ້າງແບບຈໍາລອງກໍລະນີສຶກສາ. ວິທີການທີ 1 ແມ່ນ
ໃຊ້ CRAFT
CRAFT (Computerized Relative Allocation of Facilities Technique) ໃຊ້ການແລກປ່ຽນແບບສະຫລາດຄູ່ເພື່ອພັດທະນາຮູບແບບ (Buffa et al., 1964; Hicks and Lowan, 1976). CRAFT ບໍ່ໄດ້ກວດສອບການແລກປ່ຽນຄູ່ທີ່ເປັນໄປໄດ້ທັງຫມົດກ່ອນທີ່ຈະສ້າງຮູບແບບການປັບປຸງ. ຂໍ້ມູນການປ້ອນຂໍ້ມູນປະກອບມີຂະຫນາດຂອງອາຄານແລະສິ່ງອໍານວຍຄວາມສະດວກ, ການໄຫຼເຂົ້າຂອງວັດສະດຸຫຼືຄວາມຖີ່ຂອງການເດີນທາງລະຫວ່າງຄູ່ສະຖານທີ່ແລະຄ່າໃຊ້ຈ່າຍຕໍ່ຫນ່ວຍໂຫຼດຕໍ່ໄລຍະຫ່າງ. ຜະລິດຕະພັນຂອງການໄຫຼ (f) ແລະໄລຍະຫ່າງ (d) ສະຫນອງຄ່າໃຊ້ຈ່າຍຂອງອຸປະກອນການເຄື່ອນຍ້າຍລະຫວ່າງ 2 ສະຖານທີ່. ຫຼັງຈາກນັ້ນ, ການຫຼຸດຜ່ອນຄ່າໃຊ້ຈ່າຍແມ່ນຄິດໄລ່ໂດຍອີງໃສ່ຄ່າໃຊ້ຈ່າຍໃນການຈັດການວັດສະດຸກ່ອນແລະຫຼັງການແລກປ່ຽນ.
ລໍາດັບທີ່ດີທີ່ສຸດ
ວິທີການແກ້ໄຂບັນຫາເລີ່ມຕົ້ນດ້ວຍການຈັດລໍາດັບຕາມລໍາດັບທີ່ຕົນເອງມັກແລະພະຍາຍາມປັບປຸງມັນໂດຍການປ່ຽນ 2 ພະແນກໃນລໍາດັບ (Heragu, 1997). ໃນແຕ່ລະຂັ້ນຕອນ, ວິທີການຄິດໄລ່ການປ່ຽນແປງການໄຫຼ * ໄລຍະຫ່າງສໍາລັບການປ່ຽນທີ່ເປັນໄປໄດ້ທັງຫມົດຂອງ 2 ພະແນກແລະເລືອກເອົາຄູ່ທີ່ມີປະສິດທິພາບທີ່ສຸດ. 2 ພະແນກຖືກປ່ຽນແລະວິທີການເຮັດຊ້ໍາອີກ. ຂະບວນການຢຸດເຊົາໃນເວລາທີ່ບໍ່ມີສະຫຼັບເຮັດໃຫ້ຄ່າໃຊ້ຈ່າຍຫຼຸດລົງ. ວັດສະດຸປ້ອນທີ່ຈໍາເປັນເພື່ອສ້າງໂຄງຮ່າງໂດຍໃຊ້ລໍາດັບທີ່ດີທີ່ສຸດແມ່ນຂະຫນາດຂອງອາຄານແລະສິ່ງອໍານວຍຄວາມສະດວກ, ການໄຫຼເຂົ້າຂອງວັດສະດຸຫຼືຄວາມຖີ່ຂອງການເດີນທາງລະຫວ່າງຄູ່ສະຖານທີ່ແລະຄ່າໃຊ້ຈ່າຍຕໍ່ການໂຫຼດຕໍ່ຫນ່ວຍຕໍ່ໄລຍະຫ່າງ.
ໃຊ້ BLOCPLAN
BLOCPLAN ແມ່ນໂຄງການແບບໂຕ້ຕອບທີ່ໃຊ້ເພື່ອພັດທະນາ ແລະປັບປຸງຮູບແບບຊັ້ນດຽວ ແລະຫຼາຍຊັ້ນ (ສີຂຽວ ແລະ
ສ້າງການຈັດວາງບລັອກຫຼາຍອັນ ແລະມາດຕະການການສອດຄ່ອງຂອງເຂົາເຈົ້າ. ຜູ້ໃຊ້ສາມາດເລືອກວິທີແກ້ໄຂທີ່ກ່ຽວຂ້ອງໂດຍອີງໃສ່ສະຖານະການ.
ສູດການຄິດໄລ່ທາງພັນທຸກໍາ
ມີຫຼາຍວິທີຂອງການສ້າງສິ່ງອໍານວຍຄວາມສະດວກໃນການຈັດວາງບັນຫາຜ່ານລະບົບທາງພັນທຸກໍາ (GA).Banerjee, Zhou, ແລະ Montreuil (1997) ໄດ້ນໍາໃຊ້ GA ເຂົ້າໃນການຈັດວາງຂອງເຊນ.. ໂຄງສ້າງຕົ້ນໄມ້ຖືກຕັດເປັນວິທີທີ 1 ແນະນໍາໂດຍ Otten (1982) ເປັນວິທີການເປັນຕົວແທນຂອງການຈັດປະເພດ. ວິທີການດັ່ງກ່າວໄດ້ຖືກນໍາໃຊ້ຕໍ່ມາໂດຍຜູ້ຂຽນຫຼາຍຄົນລວມທັງ Tam and Chan (1995) ຜູ້ທີ່ໃຊ້ມັນເພື່ອແກ້ໄຂບັນຫາການຈັດວາງພື້ນທີ່ທີ່ບໍ່ເທົ່າທຽມກັນກັບຂໍ້ຈໍາກັດທາງເລຂາຄະນິດ. ສູດການຄິດໄລ່ GA ທີ່ໃຊ້ໃນວຽກງານນີ້ໄດ້ຖືກພັດທະນາໂດຍ Shayan ແລະ Chittilappilli (2004) ໂດຍອີງໃສ່ໂຄງສ້າງຕົ້ນໄມ້ (STC). ມັນຂຽນລະຫັດແຜນຜັງຜູ້ສະຫມັກທີ່ມີໂຄງສ້າງຂອງຕົ້ນໄມ້ເຂົ້າໄປໃນໂຄງສ້າງພິເສດຂອງໂຄໂມໂຊມ 2 ມິຕິທີ່ສະແດງໃຫ້ເຫັນສະຖານທີ່ທີ່ກ່ຽວຂ້ອງຂອງແຕ່ລະສະຖານທີ່ຢູ່ໃນຕົ້ນໄມ້ຕັດ. ໂຄງການພິເສດແມ່ນມີໃຫ້ເພື່ອຈັດການໂຄໂມໂຊມໃນການດໍາເນີນງານ GA (Tam and Li, 1991). ການດໍາເນີນງານ "cloning" ໃຫມ່ຍັງຖືກນໍາສະເຫນີໃນ Shayan ແລະ
3. ການທົດລອງຜ່ານກໍລະນີສຶກສາ
ເພື່ອທົດສອບການປະຕິບັດຂອງວິທີການທີ່ໄດ້ອະທິບາຍໄວ້ກ່ອນ, ພວກມັນທັງຫມົດຖືກນໍາໃຊ້ກັບກໍລະນີທີ່ແທ້ຈິງໃນການຜະລິດເຟີນີເຈີ. ບໍລິສັດຜະລິດ 9 ແບບທີ່ແຕກຕ່າງກັນຂອງເກົ້າອີ້, 2- Seaters ແລະ
ແຕ່ລະຜະລິດຕະພັນຜ່ານ 11 ການດໍາເນີນງານເຊິ່ງເລີ່ມຕົ້ນຢູ່ທີ່ Facility 1 - Cutting Area ແລະສິ້ນສຸດຢູ່ທີ່ Facility 11- Bolt up Area. ແຕ່ລະສະພາແຫ່ງສຸດທ້າຍສາມາດແບ່ງອອກເປັນຊຸດຍ່ອຍທີ່ມີຊື່ດຽວກັນ. ສະພາຍ່ອຍເຫຼົ່ານີ້ພົບກັນຢູ່ທີ່ Bolt
ເນື່ອງຈາກນີ້ບໍ່ມີການໄຫຼຕາມລໍາດັບຂອງວັດສະດຸ, ເຮັດໃຫ້ການເຮັດວຽກຢູ່ໃນຄວາມຄືບຫນ້າ. ການພົວພັນລະຫວ່າງສິ່ງອໍານວຍຄວາມສະດວກສາມາດຖືກກໍານົດໂດຍໃຊ້ຫົວຂໍ້ເຊັ່ນດຽວກັນກັບມາດຕະການຈຸດປະສົງ. ວັດສະດຸປ້ອນຕົ້ນຕໍທີ່ຕ້ອງການສໍາລັບຕາຕະລາງການໄຫຼແມ່ນຄວາມຕ້ອງການ, ປະລິມານຂອງວັດສະດຸທີ່ຜະລິດແລະປະລິມານຂອງວັດສະດຸທີ່ໄຫຼລະຫວ່າງເຄື່ອງຈັກແຕ່ລະຄົນ. ການໄຫຼເຂົ້າຂອງວັດສະດຸແມ່ນຄິດໄລ່ຕາມປະລິມານການໄຫຼຂອງວັດສະດຸທີ່ເດີນທາງຕໍ່ 10 ເດືອນ * ຫົວໜ່ວຍວັດແທກທີ່ສະແດງໃນຮູບທີ 2. ຮູບທີ 3 ສະແດງເນື້ອທີ່ຂອງແຕ່ລະພະແນກທີ່ໃຊ້ໃນກໍລະນີສຶກສາ. ຮູບທີ 4 ສະແດງໃຫ້ເຫັນຮູບແບບປະຈຸບັນຂອງກໍລະນີສຶກສາ.
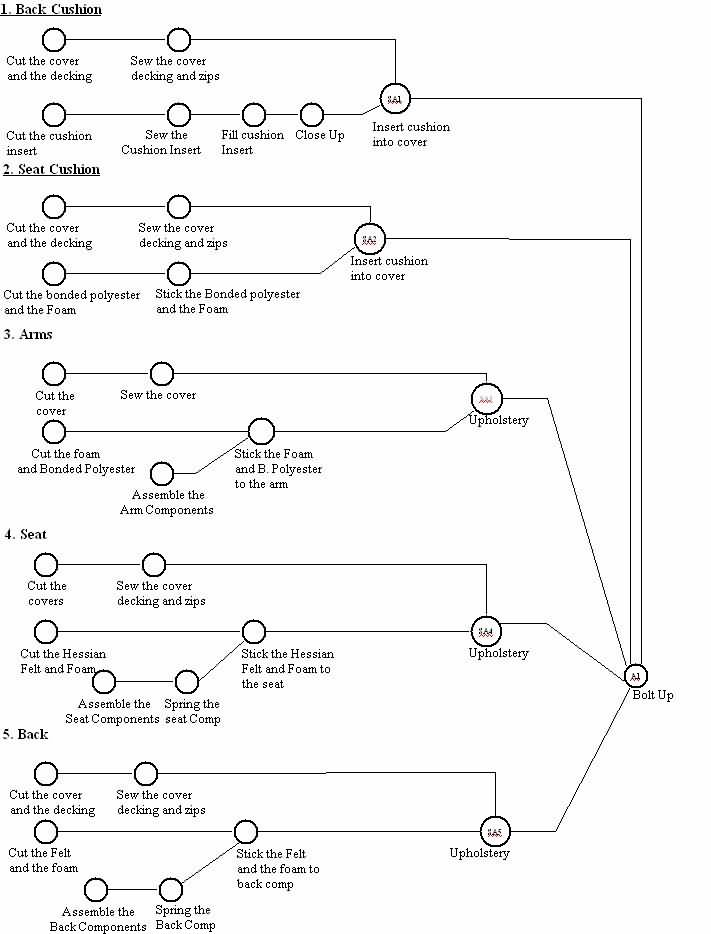
ຮູບທີ 1 ຕາຕະລາງສະພາສໍາລັບກໍລະນີສຶກສາ
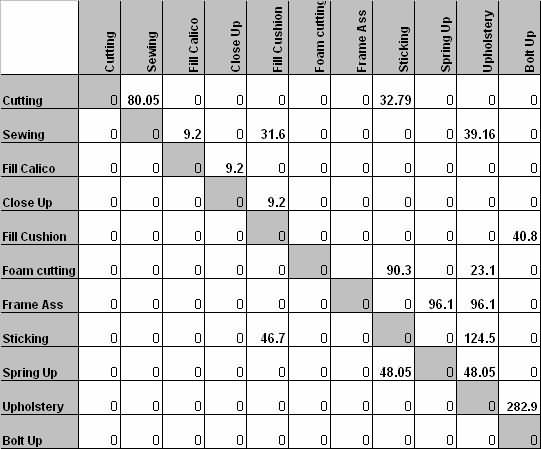
ຮູບທີ 2 ການໄຫຼເຂົ້າຂອງເອກະສານສໍາລັບກໍລະນີສຶກສາ.
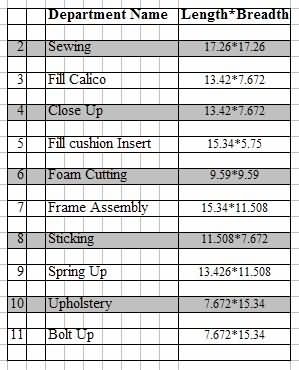
ຮູບທີ 3 ຕົວເລກທີ່ກົງກັບພະແນກ
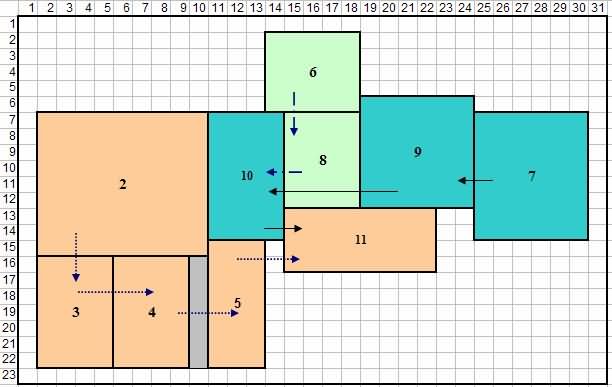
ຮູບທີ 4 ຮູບແບບປະຈຸບັນຂອງບໍລິສັດເຟີນີເຈີ ແລະ ຂະໜາດຂອງແຕ່ລະພະແນກທີ່ໃຊ້ໃນການສ້າງແບບຈຳລອງຂອງກໍລະນີສຶກສາ
4. ຄໍາຮ້ອງສະຫມັກຂອງວິທີການສ້າງແບບຈໍາລອງ
ຕໍ່ໄປນີ້ແມ່ນວິທີການສ້າງແບບຈໍາລອງຕ່າງໆທີ່ໄດ້ສົນທະນາໃນພາກທີ 2 ຖືກນໍາໃຊ້ກັບກໍລະນີສຶກສາເພື່ອສ້າງຮູບແບບທາງເລືອກສໍາລັບການປຽບທຽບ.
4.1 ການນໍາໃຊ້ທິດສະດີກາຟ
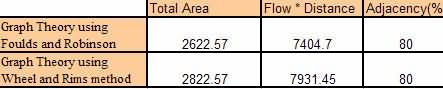
ຕາຕະລາງ 1 ສະແດງໃຫ້ເຫັນການປຽບທຽບຜົນໄດ້ຮັບໂດຍໃຊ້ 2 ວິທີການທີ່ແຕກຕ່າງກັນຂອງທິດສະດີກຣາຟຄືວິທີການ Foulds ແລະ Robinsons ແລະວິທີການ Wheels and Rims. ຕາຕະລາງ 1 ມັນສະແດງໃຫ້ເຫັນຢ່າງຊັດເຈນວ່າວິທີການ Foulds ແລະ Robinsons ແມ່ນດີກວ່າຂອງ 2 ຜົນໄດ້ຮັບ. ຜົນໄດ້ຮັບຂອງວິທີການ Foulds ແລະ Robinsons ໄດ້ຖືກອະທິບາຍຢ່າງລະອຽດໃນຕົວເລກ
ຕາຕະລາງ 1: ຕາຕະລາງສະແດງໃຫ້ເຫັນການປຽບທຽບ 2 ວິທີການທີ່ແຕກຕ່າງກັນຂອງທິດສະດີກາຟທີ່ໃຊ້.
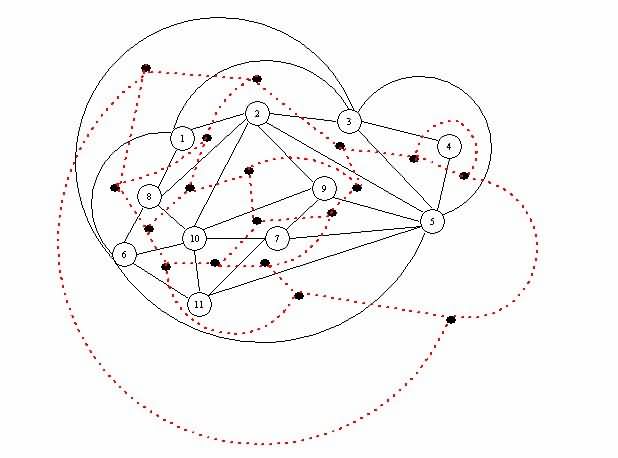
ຮູບທີ 5 ເສັ້ນສະແດງຜົນການຕິດກັນຂອງກໍລະນີສຶກສາໂດຍໃຊ້ວິທີ Foulds ແລະ Robinson.
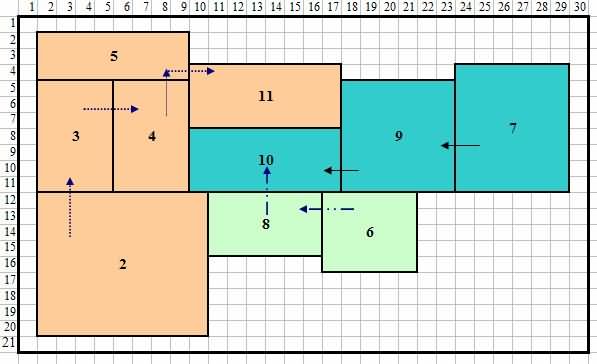
ຮູບທີ 6 ການປັບປຸງການຈັດວາງຫຼັງຈາກການນໍາໃຊ້ທິດສະດີກາຟ (ວິທີ Foulds ແລະ Robinsons)
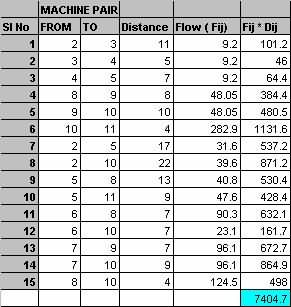
ຮູບທີ່ 7 Flow * ຕາຕະລາງການປະເມີນໄລຍະຫ່າງສໍາລັບກໍລະນີສຶກສາໂດຍໃຊ້ທິດສະດີກາຟ (Foulds ແລະ Robinsons method)
4.2 ການນຳໃຊ້ CRAFT
ຂໍ້ມູນການປ້ອນຂໍ້ມູນສໍາລັບ CRAFT ໄດ້ຖືກປ້ອນເຂົ້າ ແລະຄ່າໃຊ້ຈ່າຍເບື້ອງຕົ້ນສໍາລັບໂຄງຮ່າງປະຈຸບັນແມ່ນເປັນການຄິດໄລ່ທີ 1. ຄ່າໃຊ້ຈ່າຍນີ້ສາມາດຫຼຸດຜ່ອນການນໍາໃຊ້ການປຽບທຽບທີ່ສະຫລາດຄູ່ດັ່ງທີ່ສະແດງໃຫ້ເຫັນໃນຮູບພາບ 8,9.
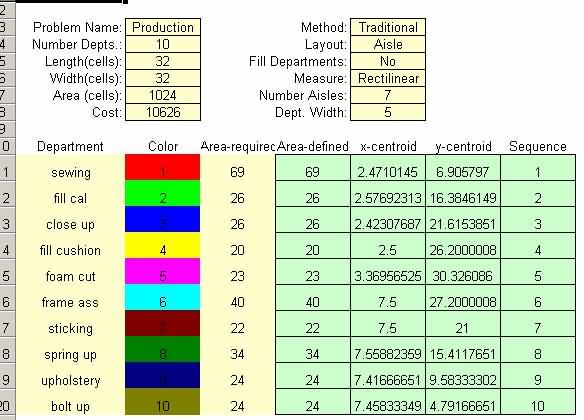
ຮູບທີ 8 ຄ່າໃຊ້ຈ່າຍເບື້ອງຕົ້ນສໍາລັບຮູບແບບປະຈຸບັນໂດຍໃຊ້ CRAFT
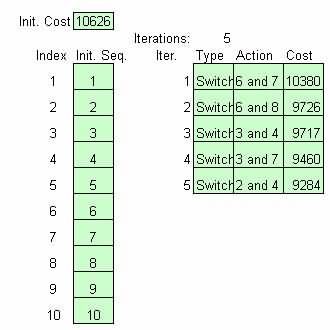
ຮູບທີ 9 ຂັ້ນຕອນການແລກປ່ຽນໂດຍ CRAFT
ຜົນໄດ້ຮັບຈາກ CRAFT ແມ່ນສະແດງຢູ່ໃນຕາຕະລາງ 2. ອີງຕາມການຄິດໄລ່ຂ້າງເທິງ, ຮູບແບບໃຫມ່ແລະການປັບປຸງສາມາດແຕ້ມໄດ້ເຊິ່ງສະແດງຢູ່ໃນຮູບ 10.
ຕາຕະລາງ 2: ຕາຕະລາງສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບ

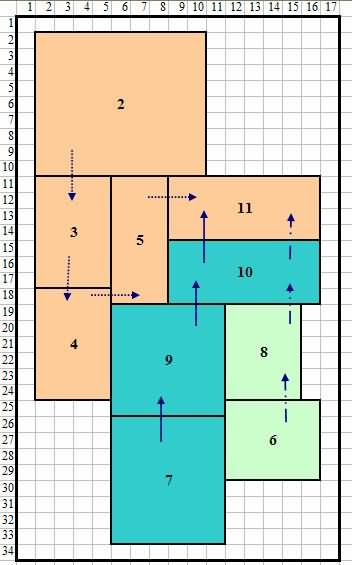
ຮູບທີ 10 ການປັບປຸງການຈັດວາງທີ່ສ້າງຂຶ້ນໂດຍ CRAFT
4.3 ຂັ້ນຕອນການລຳດັບທີ່ດີທີ່ສຸດ
ຂໍ້ມູນການປ້ອນຂໍ້ມູນແມ່ນຄືກັນກັບ CRAFT ຍົກເວັ້ນວ່າມັນປະຕິບັດຕາມຊຸດການປຽບທຽບຄູ່ທີ່ສະຫລາດ. ຕາຕະລາງ 3 ສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບຈາກຮູບແບບການປັບປຸງ. ຮູບທີ 11 ສະແດງໃຫ້ເຫັນຮູບແບບທີ່ປັບປຸງໃຫ້ດີຂຶ້ນໂດຍໃຊ້ Optimum Sequence.
ຕາຕະລາງ 3 A ຕາຕະລາງສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບໂດຍໃຊ້ CRAFT

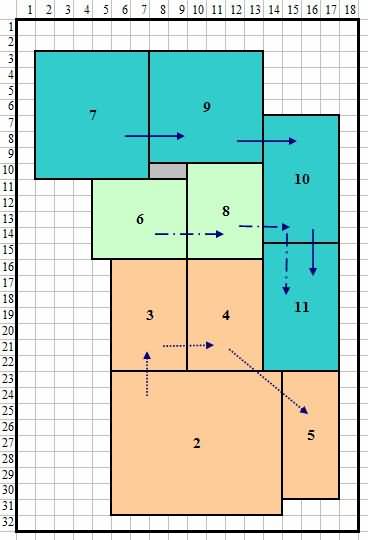
4.4 ການນໍາໃຊ້ BLOCPLAN
ຕາຕະລາງ Flow matrix ໄດ້ຖືກປ່ຽນເປັນຕາຕະລາງ REL ດັ່ງທີ່ສະແດງຢູ່ໃນຮູບ 12 ດ້ວຍຕົວກໍານົດການດັ່ງຕໍ່ໄປນີ້:

ຮູບທີ 12 ຕາຕະລາງ REL ສໍາລັບກໍລະນີສຶກສາ

ຕາຕະລາງ 4 ສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບໂດຍໃຊ້ວິທີການທີ່ແຕກຕ່າງກັນ. ດັ່ງທີ່ເຫັນ BLOCPLAN ໂດຍໃຊ້ການຄົ້ນຫາແບບອັດຕະໂນມັດໄດ້ສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບທີ່ດີກວ່າການນໍາໃຊ້ວິທີການກໍ່ສ້າງ.
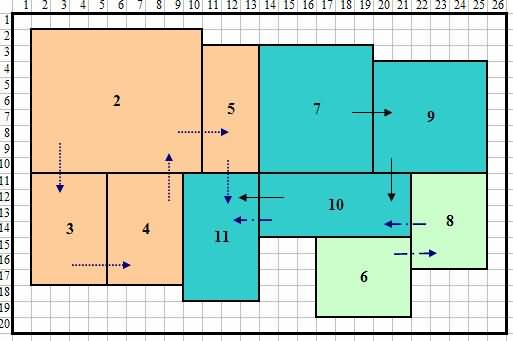
ຮູບທີ 13 ການປັບປຸງການຈັດວາງການຊອກຫາແບບອັດຕະໂນມັດ

ຕາຕະລາງ 4 ມາດຕະການສໍາລັບການຈັດວາງ BLOCPLAN
4.5 ການນໍາໃຊ້ສູດການຄິດໄລ່ທາງພັນທຸກໍາ
ການແກ້ໄຂທີ່ດີທີ່ສຸດທີ່ພົບໂດຍ algorithm ແມ່ນສະແດງຢູ່ໃນຮູບ 14. ຫຼັງຈາກນັ້ນ, ນີ້ຈະຖືກປ່ຽນເປັນຮູບແບບໃນຮູບ 15 ສໍາລັບການປຽບທຽບທົ່ວໄປກັບແບບອື່ນໆ.

ຮູບທີ 14 ແຜນຜັງພັດທະນາໂດຍວິທີທາງພັນທຸກໍາ
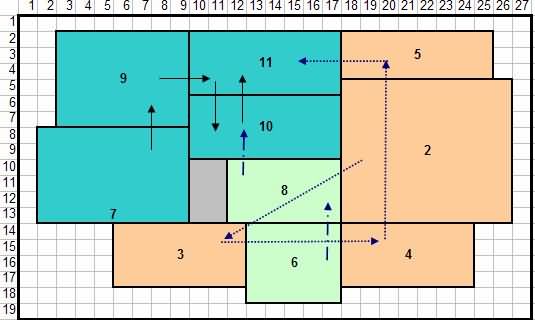
ຮູບທີ 15 ການປ່ຽນຮູບແບບໃນຮູບທີ 14
ຕາຕະລາງ 5 ສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບໂດຍໃຊ້ Genetic Algorithm.

ຕາຕະລາງ 5 ຕາຕະລາງສະແດງໃຫ້ເຫັນຜົນໄດ້ຮັບໂດຍໃຊ້ສູດການຄິດໄລ່ທາງພັນທຸກໍາ
5. ການປຽບທຽບຜົນການທົດລອງໂດຍ AHP
ຕາຕະລາງ 6 ສະຫຼຸບຜົນທີ່ໄດ້ຮັບຈາກເຕັກນິກການສ້າງແບບຈໍາລອງທັງໝົດທຽບກັບໂຄງຮ່າງປະຈຸບັນເພື່ອປຽບທຽບ. ພາກສ່ວນຂອງການຈັດວາງທີ່ດີທີ່ສຸດຈະເຮັດໄດ້ໂດຍອີງໃສ່ 3 ປັດໃຈຄື Total Area (Minimze), Flow * Distance (Maximize) ແລະ Adjacency ເປີເຊັນ (Maximize). ຈຸດປະສົງຕົ້ນຕໍແມ່ນເພື່ອຫຼຸດຜ່ອນ WIP ແລະຈັດຕັ້ງການໄຫຼເຂົ້າລະບົບຂອງວັດສະດຸ. ດັ່ງນັ້ນ, ການໄຫຼ * ໄລຍະຫ່າງ matrix ແມ່ນຕົວກໍານົດການທີ່ສໍາຄັນທີ່ສຸດ.
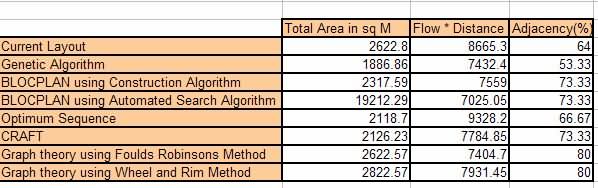
ຕາຕະລາງ 6 ສະຫຼຸບຜົນໄດ້ນໍາໃຊ້ເຕັກນິກການສ້າງແບບຈໍາລອງທັງໝົດທຽບກັບຜົນຂອງການຈັດວາງປະຈຸບັນ
ຕາຕະລາງ 7 ສະແດງໃຫ້ເຫັນການປະສົມຂອງການຈັດລໍາດັບທາງເລືອກໂດຍອີງໃສ່ປັດໃຈຕ່າງໆ. ຕົວຢ່າງ Layout 1 ມີອັນດັບທີ່ບໍ່ດີຢູ່ໃນພື້ນທີ່ແລະ F*D ໃນຂະນະທີ່ເປັນທີ່ດີທີ່ສຸດໃນ Adjacency. ການປະສົມປະສານເຮັດໃຫ້ມັນຍາກທີ່ຈະເລືອກເອົາຫນຶ່ງໃນໄລຍະອື່ນໆ. ພວກເຮົາຮຽກຮ້ອງໃຫ້ນໍາໃຊ້ເຕັກນິກທີ່ເປັນທາງການ, AHP, ປະຕິບັດໂດຍຊອຟແວທາງເລືອກຜູ້ຊ່ຽວຊານ.
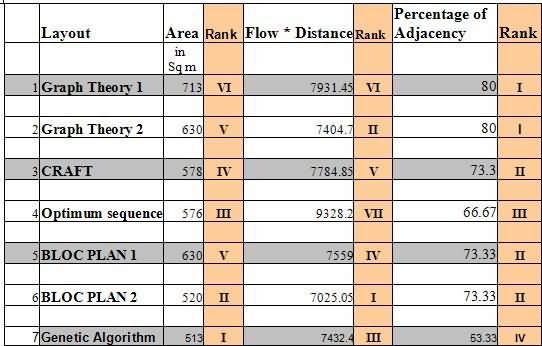
ຕາຕະລາງ 7 ການຈັດລໍາດັບທາງເລືອກຕ່າງໆກ່ຽວກັບຈຸດປະສົງ
AHP ປຽບທຽບຄວາມສຳຄັນຂອງເດັກນ້ອຍແຕ່ລະຄົນກ່ຽວກັບພໍ່ແມ່. ເມື່ອການປຽບທຽບຄູ່ສໍາເລັດແລ້ວ, ວິທີການສັງເຄາະຜົນໄດ້ຮັບໂດຍໃຊ້ບາງຕົວແບບທາງຄະນິດສາດເພື່ອກໍານົດການຈັດອັນດັບລວມ. ຮູບທີ 16 ສະແດງໃຫ້ເຫັນການຈັດອັນດັບຂອງຜົນໄດ້ຮັບທີ່ບັນລຸໄດ້ຈາກ algorithms ທັງຫມົດດ້ວຍຄວາມເຄົາລົບເປົ້າຫມາຍຂອງການແກ້ໄຂທາງເລືອກທີ່ດີທີ່ສຸດ.
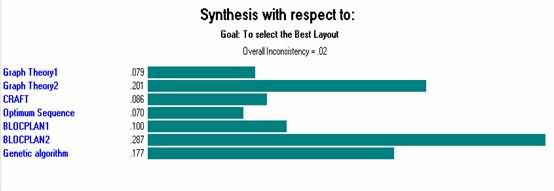
ຮູບທີ 16 ການສັງເຄາະກ່ຽວກັບເປົ້າໝາຍ
ການແກ້ໄຂທີ່ດີທີ່ສຸດແມ່ນບັນລຸໄດ້ໂດຍ BLOCPLAN (ການຊອກຫາອັດຕະໂນມັດ) ປະຕິບັດຕາມໂດຍ Graph Theory ການນໍາໃຊ້ Foulds ແລະ Robinsons Method, ຫຼັງຈາກນັ້ນວິທີການທາງພັນທຸກໍາ. ວິທີແກ້ໄຂອື່ນໆແມ່ນຮ້າຍແຮງກວ່າເກົ່າ. ໃຫ້ສັງເກດວ່າເນື່ອງຈາກການຈັດລໍາດັບຫົວຂໍ້ທີ່ປະກົດຂຶ້ນບໍ່ແມ່ນຕົວຊີ້ບອກຢ່າງແທ້ຈິງຂອງທາງເລືອກທີ່ດີກວ່າ, ແທນທີ່ຈະເປັນຄໍາແນະນໍາທີ່ຜູ້ໃຊ້ສາມາດສ້າງຄວາມບັນເທີງໃຫ້ເຫມາະສົມກັບຄວາມຕ້ອງການ.
ພວກເຮົາສະເຫນີຮູບແບບທີ່ສ້າງຂຶ້ນໂດຍໃຊ້ BLOCPLAN ໂດຍໃຊ້ການຄົ້ນຫາອັດຕະໂນມັດເປັນການແກ້ໄຂທີ່ເລືອກ. ໃນເວລາທີ່ການຕັດສິນໃຈນີ້, ການວິເຄາະຄວາມອ່ອນໄຫວໄດ້ດໍາເນີນການເພື່ອຮັບປະກັນວ່າທາງເລືອກແມ່ນເຂັ້ມແຂງ. ຖ້າເວລາອະນຸຍາດໃຫ້ນີ້ຄວນຈະເຮັດສໍາລັບທາງເລືອກທີ່ໃກ້ຊິດອື່ນໆກ່ອນທີ່ຈະເລືອກ.
6. ບົດສະຫຼຸບ
ເປົ້າຫມາຍໃນເອກະສານນີ້ແມ່ນການນໍາໃຊ້ເຕັກນິກການສ້າງແບບຈໍາລອງຕ່າງໆເພື່ອເລືອກຮູບແບບທີ່ດີທີ່ສຸດສໍາລັບບໍລິສັດເຟີນີເຈີ. ແຜນຜັງທີ່ດີທີ່ສຸດແມ່ນສ້າງຂຶ້ນໂດຍ BLOCPLAN ໂດຍໃຊ້ການຄົ້ນຫາແບບອັດຕະໂນມັດໃນຮູບ 17.
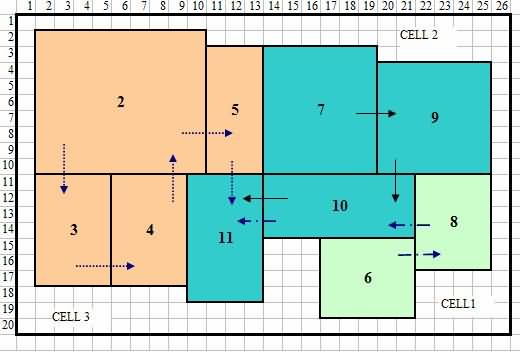
ຮູບທີ 17 ການຈັດວາງທີ່ດີທີ່ສຸດໂດຍໃຊ້ວິທີການສ້າງແບບຈໍາລອງ
ຕາຕະລາງ 9 ສະແດງໃຫ້ເຫັນການປັບປຸງການແກ້ໄຂທີ່ສະເຫນີໃນໄລຍະຮູບແບບປະຈຸບັນ. ໃຫ້ສັງເກດວ່າການຈັດວາງສະແດງຕັນແລະສະຖານທີ່ທີ່ກ່ຽວຂ້ອງຂອງພວກເຂົາ. ຂໍ້ຈໍາກັດດ້ານການປະຕິບັດຈໍາເປັນຕ້ອງໄດ້ຖືກນໍາໃຊ້ເພື່ອໃຫ້ເຫມາະສົມກັບຄວາມຕ້ອງການທັງຫມົດ. ຫຼັງຈາກນັ້ນ, ລາຍລະອຽດເພີ່ມເຕີມຂອງແຕ່ລະຕັນສາມາດວາງແຜນ, ຖ້າຈໍາເປັນໃນລັກສະນະດຽວກັນ.

ຕາຕະລາງ 9: ການປັບປຸງຮູບແບບໃນປະຈຸບັນໂດຍໃຊ້ເຕັກນິກການສ້າງແບບຈໍາລອງ
ຜົນໄດ້ຮັບແມ່ນຂ້ອນຂ້າງພໍໃຈກັບບໍລິສັດ, ເຊິ່ງບໍ່ມີຄວາມຮູ້ກ່ຽວກັບວິທີການວິທະຍາສາດ.



